fft总结

引入

对于两个多项式，我们可以在 O(n2)O(n^2) 的时间复杂度内求出他们的乘积（即卷积）

但如果 n≤106n\le 10^6 呢？

那就用FFT吧~

FFT就是 O(nlog⁡n)O(n\log n) 求两个多项式乘积的东西

系数与点值表示

系数表示

对于一个多项式 f(x)=a0+a1x+a2x2+...anxnf(x)=a_0+a_1x+a_2x^2+...a_nx^n，我们可以把它的每一项系数提出来，变为

(a0,a1,a2...,an)(a_0,a_1,a_2...,a_n)

这就是多项式的系数表示

点值表示

众所周知，n+1n+1 个点可以确定一个 nn 次函数

那么就可以用 n+1n+1 个点表示一个 nn 次函数

这就是多项式的点值表示

那既然系数乘法要 O(n2)O(n^2) 的复杂度，点值的乘法又是 O(n)O(n) 的

则我们可考虑系数表示化为点值表示

这样我们就只需要一个能快速将多项式转换为点值表示和快速将点值表示转换为多项式的算法了

单位根

定义

对于方程 xn=1x^n=1，它的解就相当于复平面上单位圆上的 nn 个 nn 等分点，如当 n=3n=3 时

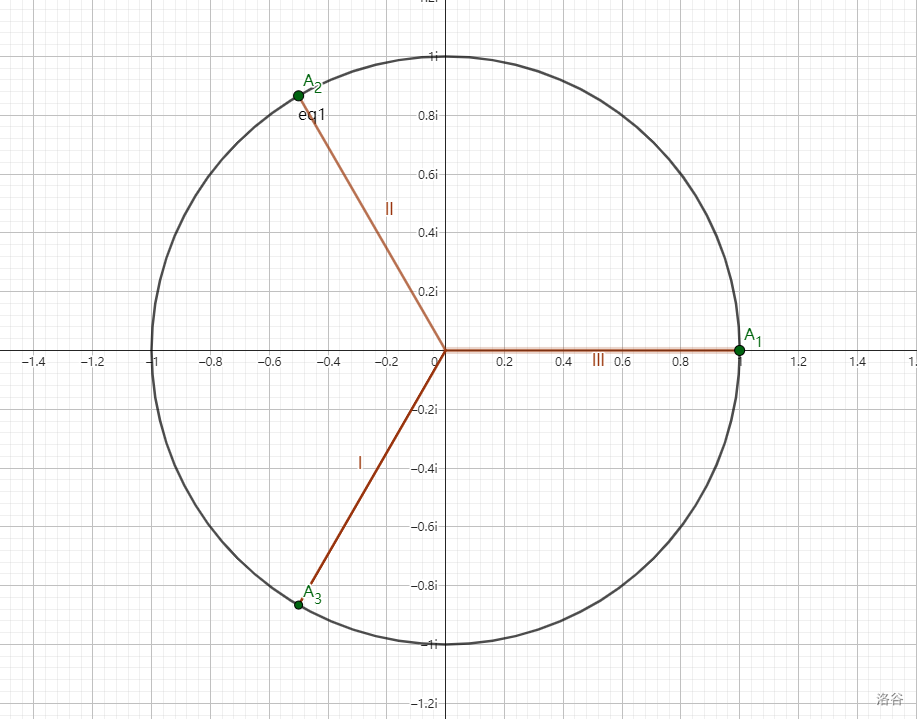
图中 A1,A2,A3A_1,A_2,A_3 三点即为 x3=1x^3=1 的解

设幅角为正且最小的复数为 ωn\omega_n，称为 nn 次单位根，即
ωn=cos⁡(2πn)+isin⁡(2πn)\omega_n=\cos\left(\frac{2\pi}{n}\right)+i\sin\left(\frac{2\pi}{n}\right)
即为图中 A2A_2 点的坐标

由欧拉公式
ωnk=cos⁡(2kπn)+isin⁡(2kπn)\omega_n^k=\cos\left(\frac{2k\pi}{n}\right)+i\sin\left(\frac{2k\pi}{n}\right)

性质

ωn‾=cos⁡(2πn)−isin⁡(2πn)\overline{\omega_n} =\cos\left(\frac{2\pi}{n}\right)-i\sin\left(\frac{2\pi}{n}\right)
ωanak=cos⁡(2akπn)+isin⁡(2akπn)=cos⁡(2kπn)+isin⁡(2kπn)=ωnk\omega_{an}^{ak} =\cos\left(\frac{2ak\pi}{n}\right)+i\sin\left(\frac{2ak\pi}{n}\right) =\cos\left(\frac{2k\pi}{n}\right)+i\sin\left(\frac{2k\pi}{n}\right) =\omega_n^k

FFT

FFT就是在 O(nlog⁡n)O(n\log n) 的时间复杂度内算出多项式的点值表示

对于多项式 f(x)=a0+a1x+a2x2+...+an−1xn−1f(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}

我们要将其转化为点值表示，可以设 n=2kn=2^k（即在高次项处补0),那么我们可以按照次数的奇偶性分为：
f(x)=(a0+a2x2+...+an−2xn−2)+(a1x+a3x3+...+an−1xn−1)f(x)=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+(a_1x+a_3x^3+...+a_{n-1}x^{n-1})
设
f1(x)=a0+a2x+a4x2+...+an−2xn2f_1(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac{n}{2}}
f2(x)=a1+a3x+a5x2+...+an−1xn2f_2(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac{n}{2}}
则
f(x)=f1(x2)+xf2(x2)f(x)=f_1(x^2)+xf_2(x^2)
f(−x)=f1(x2)−xf2(x2)f(-x)=f_1(x^2)-xf_2(x^2)

对于 f1(x)f_1(x) 和 f2(x)f_2(x),我们也可以如法炮制

那 xx 我们应该带入什么值呢？

既然都讲了 ωn\omega_n 那就带 ωn\omega_n 吧（其实是因为 ωn\omega_n 好算，且 ωanak=ωnk\omega_{an}^{ak}=\omega_n^k）

所以
f(ωn)=f1(ωn2)+ωnf2(ωn2)=f1(ωn2)+ωnf2(ωn2)f(\omega_n) =f_1(\omega_n^2)+\omega_nf_2(\omega_n^2) =f_1(\omega_{\frac{n}{2}})+\omega_nf_2(\omega_{\frac{n}{2}})

f(−ωn)=f1(ωn2)−ωnf2(ωn2)=f1(ωn2)−ωnf2(ωn2)f(-\omega_n) =f_1(\omega_n^2)-\omega_nf_2(\omega_n^2) =f_1(\omega_{\frac{n}{2}})-\omega_nf_2(\omega_{\frac{n}{2}})
最后就可以分治来算了，时间复杂度 O(nlog⁡n)O(n\log n)

代码

struct complex
{
	double r,i;
	complex operator +(complex a)
	{
		a.r+=r;
		a.i+=i;
		return a;
	}
	complex operator -(complex a)
	{
		a.r-=r;
		a.i-=i;
		a.r=-a.r;
		a.i=-a.i;
		return a;
	}
	complex operator *(complex a)
	{
		double s=a.r,x=a.i;
		a.r=r*s-i*x;
		a.i=r*x+i*s;
		return a;
	}
	complex(){}
	complex(double a,double b){r=a,i=b;}
	void om(long long n)
	{
		r=cos(2*pi/n);
		i=sin(2*pi/n);
	}
};
void fft(complex s[],long long n)
{
	if(n==1) return;
	complex j[n/2+1],o[n/2+1];
	for(int i=0;i<n;i++)
	{
		if(i%2==1) j[i/2]=s[i];
		else o[i/2]=s[i];
	}
	fft(j,n/2);
	fft(o,n/2);
	complex w;
	w.om(n);
	complex c(1,0);
	for(int i=0;i<=n/2;i++,c=c*w)
	{
		s[i]=o[i]+c*j[i];
		s[n-i]=o[i]-c*j[i];
	}
}

IFFT

IFFT就是在 O(nlog⁡n)O(n\log n) 的时间复杂度内算出多项式的系数表示

那怎么做呢？就把原来变换中的 ωn\omega_n 变为它的共轭复数，即 ωn‾\overline{\omega_n}

至于为什么嘛，我也不知道为什么qwq

struct complex
{
	double r,i;
	complex operator +(complex a)
	{
		a.r+=r;
		a.i+=i;
		return a;
	}
	complex operator -(complex a)
	{
		a.r-=r;
		a.i-=i;
		a.r=-a.r;
		a.i=-a.i;
		return a;
	}
	complex operator *(complex a)
	{
		double s=a.r,x=a.i;
		a.r=r*s-i*x;
		a.i=r*x+i*s;
		return a;
	}
	complex(){}
	complex(double a,double b){r=a,i=b;}
	void om(long long n)
	{
		r=cos(2*pi/n);
		i=sin(2*pi/n);
	}
	void uom(long long n)
	{
		r=cos(2*pi/n);
		i=-sin(2*pi/n);
	}
};
void fft(complex s[],long long n,bool ifft)
{
	if(n==1) return;
	complex j[n/2+1],o[n/2+1];
	for(int i=0;i<n;i++)
	{
		if(i%2==1) j[i/2]=s[i];
		else o[i/2]=s[i];
	}
	fft(j,n/2,ifft);
	fft(o,n/2,ifft);
	complex w;
	if(ifft) w.uom(n);
	else w.om(n);
	complex c(1,0);
	for(int i=0;i<=n/2;i++,c=c*w)
	{
		s[i]=o[i]+c*j[i];
		s[n-i]=o[i]-c*j[i];
	}
}

优化

emm,(q_q)我不会