可并堆总结

左偏树

介绍

左偏树是是一种可以快速合并的堆
支持：

• $O(\log_2n)$ 插入

• $O(1)$ 查询最小值（最大值）

• $O(\log_2n)$ 删除最小值（最大值）

• $O(\log_2n)$ 合并两个堆

最重要的是，它可以可持久化

性质

左偏树的节点上存着两个值：val和dis

val即为当前节点的值

dis为维护堆“左偏”性质的值：

• 空节点的dis为0
• 左子树或右子树为空的节点dis为1
• 其余节点的dis为左右儿子dis的最小值+1

“左偏”性质为：任意一个节点左儿子的dis大于右儿子的dis

当然，你也可以“右偏”

维护左偏性质是为了使合并时复杂度降低

（也可以不维护dis，用随机数维护，后文会讲）

实现

合并

合并是左偏树中最精髓的操作

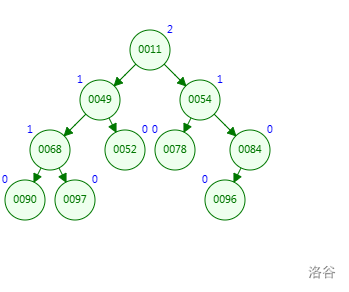
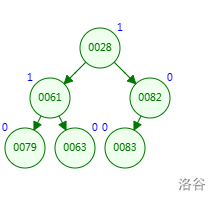
如图为两棵要合并的左偏树

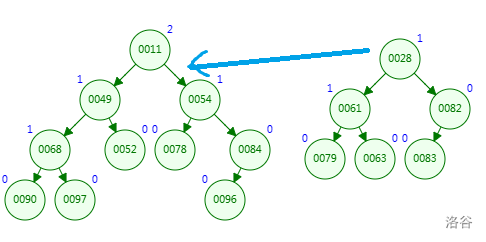
先在左子树找到能插入的地方

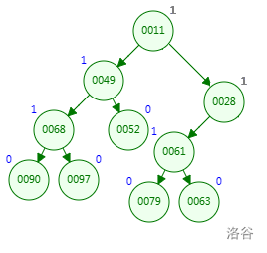
接着将合并过去的树的根节点连同右子树插入

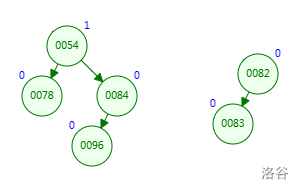
再递归合并剩下两个子树

返回时更新dis，并维护“左偏”性质

代码如下：

struct node
{
	long long a,ls,rs,fa,dis;
	bool del;
}lh[110000];
long long merge(long long x,long long y)
{
	if(x==0||y==0) return max(x,y);
	if(lh[x].a>lh[y].a) swap(x,y);
	lh[x].rs=merge(lh[x].rs,y);
	lh[lh[x].rs].fa=x;
	if(lh[lh[x].ls].dis<lh[lh[x].rs].dis) swap(lh[x].ls,lh[x].rs);
	lh[x].dis=lh[lh[x].rs].dis+1;
	return x;
}

插入

相当于把一棵只有一个节点的树与原树合并

查询最小值（最大值）

可以暴力往上跳父亲，为 $O(\log_2n)$，最坏 $O(n)$，不过最好用并查集维护

代码：

struct node
{
	long long a,ls,rs,fa,dis;
	bool del;
}lh[110000];
long long idx,n,m,fa[110000];
long long find(long long x)
{
	long long a=x;
	while(fa[a]!=a)
	{
		a=fa[a];
	}
	while(fa[x]!=x)
	{
		long long u=x;
		x=fa[x];
		fa[u]=a;
	}
	return a;
}
long long merge(long long x,long long y)
{
	if(x==0||y==0) return max(x,y);
	if(lh[x].a>lh[y].a) swap(x,y);
	lh[x].rs=merge(lh[x].rs,y);
	lh[lh[x].rs].fa=x;
	if(lh[lh[x].ls].dis<lh[lh[x].rs].dis) swap(lh[x].ls,lh[x].rs);
	lh[x].dis=lh[lh[x].rs].dis+1;
	fa[lh[x].ls]=fa[lh[x].rs]=fa[x]=x;//并查集
	return x;
}

删除

相当于把根节点的左右子树合并

void del(long long x)
{
	lh[x].del=true;
	fa[lh[x].ls]=lh[x].ls;
	fa[lh[x].rs]=lh[x].rs;
	fa[x]=merge(lh[x].ls,lh[x].rs);
}

随机合并

这时不用维护dis了，随机旋转，均摊 $O(\log_2n)$

struct node
{
	long long a,ls,rs,fa;
	bool del;
}lh[110000];
long long idx,n,m,fa[110000];
long long find(long long x)
{
	long long a=x;
	while(fa[a]!=a)
	{
		a=fa[a];
	}
	while(fa[x]!=x)
	{
		long long u=x;
		x=fa[x];
		fa[u]=a;
	}
	return a;
}
long long merge(long long x,long long y)
{
	if(x==0||y==0) return max(x,y);
	if(lh[x].a>lh[y].a) swap(x,y);
	lh[x].rs=merge(lh[x].rs,y);
	lh[lh[x].rs].fa=x;
	if(rand()%2==1) swap(lh[x].ls,lh[x].rs);
	fa[lh[x].ls]=fa[lh[x].rs]=fa[x]=x;//并查集
	return x;
}

可持久化

我不会，以后再写。

上一页