莫比乌斯函数总结

引入

偏序关系

偏序关系是一种定义在集合上的二元关系，它具有自反性、反对称性和传递性。

1、自反性（Reflexivity）: 自反性要求集合中的每个元素都和自己具有偏序关系。用符号表示就是对于集合 $A$ 中的所有元素 $a$，都有 $a \preccurlyeq a$。这意味着在任何偏序集中，每个元素都是自己的“前驱”。

2、反对称性（Antisymmetry）: 反对称性意味着如果两个元素相互之间可以比较，并且它们是相互的“前驱”，那么这两个元素必须是相同的。用符号表示就是如果 $a \preccurlyeq b$ 且 $b \preccurlyeq a$，那么 $a$ 必须等于 $b$。这排除了偏序集中存在“双向不等式”的可能性。

3、传递性（Transitivity）: 传递性要求如果$a \preccurlyeq b$ 且 $b \preccurlyeq c$，那么 $a \preccurlyeq c$ 。这意味着偏序集中的“前驱”关系是可以传递的。如果 $a$ 是 $b$ 的“前驱”，$b$ 是 $c$ 的“前驱”，那么 $a$ 也必须是 $c$ 的“前驱”。

例子：实数集上的 $\leqslant$ 关系、集合的子集关系、整数集上的整除关系

哈斯图

可比性：两个元素具有偏序关系，要么 $a<b$,要么 $b<a$，则称为 $a$ 和 $b$ 可比。否则称为不可比。例如 $(\Z+,\mid)$ 中，$2$ 不能整除 $5$，$2$ 和 $5$ 就是不可比的。

覆盖关系：$(S,<)$ 是一个偏序关系，若存在 $x<y$，其中不存在 $z$ 使得 $x<z<y$，则称 $y$ 覆盖 $x$。所有满足 $y$ 覆盖 $x$ 的有序对组成的集合称为 $(S,<)$ 的覆盖关系。哈斯图表示的就是 $(S,<)$ 覆盖关系，从下到上，低层的元素和高层的元素假如有边，则那个低层的元素为 $<$ 左边（可以叫做小于）的元素，高层的元素为 $<$ 右边（可以叫做大于）的元素，每一层元素都是不可比的。

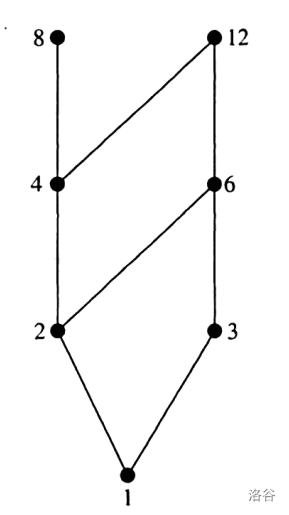
哈斯图的理解
如果我们用 $f(x)$ 表示单独的节点 $x$，$F[x]$ 表示最底部节点到 $x$ 节点所有
路径上的节点集合。

用 $f(x)$ 表示 $F[x]$，则以下 $F[x]$ 的值分别为多少？

$F[6]=f(1)+f(2)+f(3)+f(6)$

$F[12]=f(1)+f(2)+f(3)+f(4)+f(6)$

用 $F(x)$ 表示 $f[x]$，则以下 $f[x]$ 的值分别为多少？

$f[6]=F[6]-F[2]-F[3]+F[1]$

$f[12]=F[12]-F[6]-F[4]+F[2]$

规律总结：与最顶端节点距离为1的节点进行减操作，再结合容斥原理进行其他节点
操作。

以上就是从ppt里拷贝来的长篇大论内容

正文

公式兼性质一

$$F(n)=\sum_{d \mid n}f(d) \Rightarrow f(n)=\sum_{d \mid n}\mu(d)F(\frac{n}{d})$$

其中 $\mu(d)$ 为莫比乌斯函数，定义如下：

(1)若 $d=1$ 则 $\mu(d)=1$

(2)若 $d=p_1p_2...p_k$，$p_i$为互异素数，那么 $\mu(d)=(-1)^k$

(3)其他情况下 $\mu(d)=0$

证明：
建议先看性质二

$$\sum_{d \mid n}\mu(d)F(\frac{n}{d})=\sum_{d \mid n}\mu(d)\sum_{k\mid\frac{n}{d}}f(k)=\sum_{k \mid n}f(k)\sum_{d \mid \frac{n}{k}}\mu(d)$$

由性质二，当 $k \ne n$ 时，$\frac{n}{k} \ne 1$，所以$\sum_{d \mid \frac{n}{k}}\mu(d)=0$

当 $k = n$ 时，$\frac{n}{k} = 1$，所以$\sum_{d \mid \frac{n}{k}}\mu(d)=1$，所以原式结果为 $f(n)$

性质二

$$\sum_{d \mid n}\mu(d)= \begin{cases} 1\ \ (n=1)\\ 0\ \ (n>1) \end{cases}$$

证明：

当 $n=1$ 时显然成立

当 $n \ne 1$ 时，设 $n=p_{1}^{k_1}p_{2}^{k_2}...p_{n}^{k_n}$

在 $n$ 的所有因数中，$\mu$ 值不为 $0$ 只有所有质因子的次数都为 $1$ 的因数。（由 $\mu$ 的定义中可知)

设 $d$ 有 $a$ 个质因子，则这样的 $d$ 共有 $C_n^a$ 个

所以

$$\sum_{d \mid n}\mu(d)=C_n^0-C_n^1+...+(-1)^kC_n^n=\sum_{i=0}^{n}(-1)^iC_n^i$$

这个东西很明显就像二项式定理呀:
$$(a+b)^n=\sum_{i=0}^{n}C_n^ia^ib^{n-i}$$
所以带入 $a=-1,b=1$ 即得
$$(-1+1)^n=\sum_{i=0}^{n}C_n^i(-1)^i1^{n-i}=\sum_{i=0}^{n}(-1)^iC_n^i=0$$

性质三

$$\sum_{d \mid n}\frac{\mu(d)}{d}=\frac{\varphi(n)}{n}$$

证明：
因欧拉函数性质：
$$\sum_{d \mid n}\varphi(d)=n$$

所以满足

$$\varphi(n)=\sum_{d \mid n}\mu(d)\frac{n}{d}$$

两边同时除以 $n$，得

$$\sum_{d \mid n}\frac{\mu(d)}{d}=\frac{\varphi(n)}{n}$$

性质四

莫比乌斯函数为积性函数，即对于任意互质的 $a$ 和 $b$，都有
$$\mu(ab)=\mu(a) \times \mu(b)$$

证明：

设 $a=p_{1}^{k_1}p_{2}^{k_2}...p_{n}^{k_n}$

若 $k_i>1$，则结论显然成立

否则 $a=p_1p_2...p_n$,设 $b=q_1q_2...q_m(p_i,q_j为互异素数)$ 则：

$\mu(ab)\\$
$=\mu(p_1p_2...p_nq_1q_2...q_m)\\$
$=(-1)^{m+n}\\$
$=(-1)^n \times (-1)^m\\$
$=\mu(a) \times \mu(b)$

求法

可以用质因数分解求单个，也可以线性筛求多个

线性筛

long long mu[],prime[],idx;
bool isprime[];
void shai(long long n)
{
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!isprime[i])
        {
            prime[++idx]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=idx&&i*prime[j]<=n;j++)
        {
            isprime[i*prime[j]]=true;
            if(i%prime[j]==0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            mu[i*prime[j]]=-mu[i];
        }
    }
}

上一页